22 December 2018

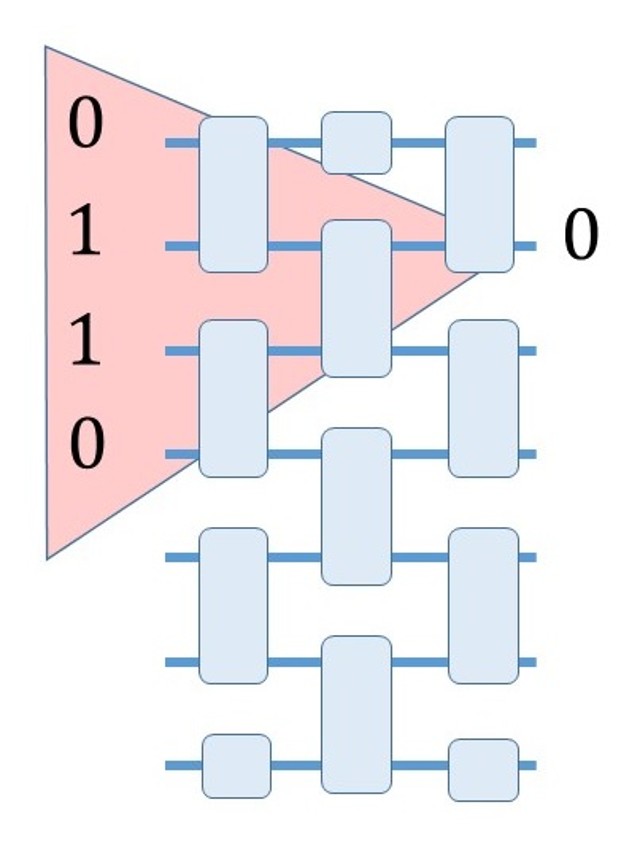
Quantum advantage with shallow circuits

In a paper published in Science [1], MQC member Robert König and collaborators from IBM and the University of Waterloo present the first unconditional separation between analogously defined classical and quantum complexity classes. In contrast, earlier arguments for the power of quantum computation relied on complexity-theoretic conjectures or were restricted to the so-called oracle model.

The paper gives a computational (linear algebra) problem which can be solved with certainty using a constant-depth quantum circuit. On the other hand, it is shown that any classical circuit which solves the problem with bounded error must have depth increasing logarithmically with the problem size.

The proposed quantum circuit only requires geometrically local gates on a 2D array of qubits, and thus appears to be a candidate for near-future experimental demonstrations of such a quantum advantage.

Publication

TUM News release